Planar graphs are sparse: any planar graph with \(n\) vertices has at most \(3n-6\) edges. A simple corollary of this sparsity is that planar graphs are \(6\)-colorable. There is simple and beautiful proof based on the Euler formula, which can easily be exteded to bounded genus graphs, a more general case: any graph embedddable in orientable surfaces of genus \(g\) with \(n\) vertices has at most \(3n + 6g-6\) edges.
How’s about the number of edges of \(K_r\)-minor-free graphs? This is a very challenging question. A reasonable speculation is \(O(r)\cdot n\): a disjoint union of \(n/(r-1)\) copies of \(K_{r-1}\) excludes a \(K_r\) minor and has \(\Theta(r)\cdot n\) edges. But this isn’t the case. And surprisingly, the correct bound is \(O(r\sqrt{\log r})n\), which will be the topic of this post.
Theorem 1: Any \(K_r\)-minor-free graphs with \(n\) vertices has at most \(O(r\sqrt{\log r})\cdot n\) edges.
The bound in Theorem 1 is tight; see a lower bound in Section 4. The sparsity bound, which is the ratio of the number of edges to the number of vertices, \(O(r\sqrt{\log r})\) was first discovered by Kostochka [4]; the proof is quite non-trivial, so as other follow-up proofs. A short proof was just found recently by Alon, Krivelevich, and Sudakov (AKS) [1], which I will present here in Section 3. See the bibliographical notes section for a detailed discussion of other proofs.
The goal of this post isn’t just to present the proof of Theorem 1. At various points in the past, I am interested in a more intuitive proof that gives good enough sparsity bounds, say \(O(\mathrm{poly}(r))\), or even \(O(f(r))\) bound for any function that depends on \(r\) only. This post describes different proofs, of increasing complexity (or ingenuity), giving different bounds. In particular, sparsity bound $2^{r}$ follows by a simple induction. Sparsity bound \(O(r^2)\) relies crucially on the fact that a graph of sparsity \(d\) has a highly connected minor of small size; the high connectivity allows us to show that for any vertex subset of size \(k \approx \sqrt{d}\) has \({k \choose 2}\) internally vertex-disjoint paths connecting these vertices, thereby giving us a \(K_{\sqrt{d}}\) minor. The optimlal bound \(O(r\sqrt{\log r})\) also relies on a highly connected minor of small size, but employs a clever probabilistic argument to construct a \(K_{r}\) minor.
1. Exponential Sparsity: \(2^{r}\)
I learn a beatiful proof of the following theorem in the graph theory book of Reinhard Diestel (Proposition 7.2.1. [3]).
Theorem 2: Any \(K_r\)-minor-free graphs with \(n\) vertices has at most \(2^{r-1}\cdot n\) edges.
Proof: Let \(G\) be a \(K_r\)-minor-free graph with \(n\) vertices. The proof is by induction on \( \vert V(G) \vert + r\). If there is a vertex \(v\) of degree at most \(2^{r-1}\), then by removing \(v\) and applying the induction hypothesis, we are done. Now consider the case where every vertex has degree more than \(2^{r-1}\); let \(v\) be such a vertex. The key idea is to find an edge \((u,v)\) such that \(u\) and \(v\) share only a few neighbors. We then contract \((u,v)\) and apply induction.
Claim 1: There is a neighbor \(u\) of \(v\) such that \( \vert N_G(v)\cap N_G(u) \vert \leq 2^{r-1}-1\).
Suppose that the claim holds, then let \(G’\) be the graph obtained from \(G\) by contracting \((u,v)\), i.e., \(G’= G/(u,v)\). Then \( \vert V(G’) \vert \leq r-1\) and \( \vert E(G’) \vert \geq \vert E(G) \vert - 2^{r-1}\). By induction, \( \vert E(G’) \vert \leq 2^{r-1}(n-1)\), which implies \( \vert E(G) \vert \leq 2^{r-1}(n-1) + 2^{r-1} = 2^{r-1}\cdot n\) as desired.
We now turn to Claim 1. Let \(H = G[N_G(v)]\) be the sugraph induced by \(N_G(v)\). Then \(H\) is \(K_{r-1}\)-minor-free. By induction, \( \vert E(H) \vert \leq 2^{r-2}\cdot \vert V(H) \vert \). Thus, there exists a vertex \(u\in H\) such that \(d_H(u) \leq 2 \vert E(H) \vert / \vert V(H) \vert \leq 2^{r-1}\). This gives \( \vert N_G(v)\cap N_G(u) \vert \leq d_H(u)-1 = 2^{r-1}-1\).
The exponential term \(2^{r-1}\) in the above theorem is due to a loss of a factor of \(2\) in each step of the induction by using \(d_H(v) \leq 2( \vert E(H) \vert / \vert V(H) \vert )\).
2. Polynomial Sparsity: \(O(r^2)\)
The goal of this section is to improve the exponential bound in Theorem 2 to a polynomial bound.
Theorem 3: Any \(K_r\)-minor-free graphs with \(n\) vertices has at most \(O(r^2)\cdot n\) edges.
Proving Theorem 3 requires a deeper understanding of the structures of minor-free graphs. The key insight is that any graph with at least \(d\cdot n\) edges has a minor, say \(K\), of \(O(d)\) size that is highly connected (Lemmas 1 and 2 below). Then we then show that given any set of vertices, say \(R\), of size about \(\Theta(\sqrt{d})\) in \(K\), we can find a collection of pairwise disjoint paths of \(H\) connecting every pair of vertices in \(R\) (due to high connectivity), which gives us a clique minor of size \(\Theta(\sqrt{d})\) (Lemma 3). Taking contrapositive gives Theorem 3.
Let \(\varepsilon(G) = \vert E(G) \vert / \vert V(G) \vert \) and \(\delta(G)\) be the minimum degree of \(G\). Fist, we show that \(G\) contains a minor of size \(\leq 2d\) and minimum degree at least \(d\).
Lemma 1: Let \(G\) be any graph of \(n\) vertices such that \( \vert E(G) \vert \geq d\cdot n\). Then \(G\) has a minor \(H\) such that \(\delta(H)\geq d \geq \vert V(H) \vert /2\).
Proof: Let \(K\) be a minimal minor of \(G\) such that \(\varepsilon(K)\geq d\). The minimality implies two properties:
- \( \vert N_K(u)\cap N_K(v) \vert \geq d\) for every edge \((u,v)\); otherwise, we can contract edge \((u,v)\).
- There exists a vertex \(x\) such that \(d_K(x)\leq 2d\); otherwise, we can delete an edge from \(K\).
Then \(H = K[N_K(x)]\) satisfying the lemma.
Next, we show that \(H\) has a highly connected subgraph.
Lemma 2: Let \(H\) be such that \(\delta(H)\geq d \geq \vert V(H) \vert /2\). Then \(H\) has a subgraph \(K\) that has (i) \( \vert V(K) \vert \leq 2d\) and (ii) \(K\) is \(d/3\)-vertex connected.
Proof: If \(H\) is \(d/3\)-vertex connected, then \(K = H\). Otherwise, there is a set \(S\subseteq V(H)\) of size at most \(d/3\) such that \(H\setminus S\) has at least two connected components. Let \(K\) be the smallest connected component of \(H\). Then \( \vert V(K) \vert \leq \vert V(H) \vert /2\leq d\) and \(\delta(K)\geq \delta(H) - \vert S \vert \geq 2d/3\). Thus, for every \(u\not= v\in K\), \(u\) and \(v\) must share at least \( \vert N_K(u) \vert + \vert N_K(v) \vert - \vert V(K) \vert \geq d/3\) neighbors in \(K\). That is, \(K\) is \(d/3\)-vertex connected.
A detour: diameter of highly connected graphs. Graph \(K\) in Lemma 2 has another nice property: its diameter is at most \(7\). To see this, suppose that there is a shortest path \({v_0,v_1,\ldots,v_8, \ldots}\) of length at least \(8\). Consider three vertices \(v_1,v_4, v_7\). Then \(N_{K}(v_1),N_{K}(v_4), N_{K}(v_7)\) are pairwise disjoint. As \(K\) is \(d/3\)-connected, \(\delta(K)\geq 3\). Thus, \( \vert N_{K}(v_1)\cup N_{K}(v_4) \cup N_{K}(v_7) \vert \geq 3(d/3+1) > d\geq V(K)\), a contradiction. We will use the same kind of arguments in several proofs below.
We now construct a minor of size \(\Theta(\sqrt{d})\) for graph \(K\) in Lemma 2. We do so by showing that for any given \(p \leq d/40\) distinct pairs of vertices \({(s_1,t_1, \ldots, (s_p,t_p)}\) in \(K\) (two pairs might share the same vertex), then there are \(p\) internally vertex-disjoint paths connecting them (Lemma 3). (Two paths are internally vertex-disjoint if they can only share endpoints.) Then one can construct a minor of size \(\sqrt{d/40}\) by picking an arbitrary set \(R\) of \(\sqrt{d/40}\) vertices, and connect all pairs of vertices in \(R\) using disjoint paths in Lemma 3, which implies Theorem 3.

Figure 1: (a) \(\mathcal{P}\) includes two paths of black edges. (b) deleting \(\mathcal{P}\) except \(s_1,t_1\). (c) \(v\) could not have more than 3 neighbors on the path from \(s_i\) to \(t_i\)
Lemma 3: Let \(\mathcal{T} = {(s_1,t_1), \ldots, (s_p,t_p)}\) be any \(p \leq d/40\) distinct pairs of vertices in \(K\) (in Lemma 2). Then there are \(p\) internally vertex-disjoint paths connecting the all pairs in \(\mathcal{T}\).
Proof: Let \(\mathcal{P}\) be a set of internally vertex-disjoint paths, each of of length at most \(10\), that connects a maximal number of pairs in \(\mathcal{T}\). Subject to the pairs connected by \(\mathcal{P}\), we choose \(\mathcal{P}\) such that the total number of edges of paths in \(\mathcal{P}\) is minimal. If \(\mathcal{P}\) connects every pair, we are done. Otherwise, w.l.o.g, we assume that \(s_1\) and \(t_1\) are not connected by \(\mathcal{P}\). See Figure 1(a).
Let \(K^-\) be obtained from \(K\) be removing all vertices in \(\mathcal{P}\), except \(s_1\) and \(t_1\), from \(K\). See Figure 1(b). Observe that the total number of vertices in \(\mathcal{P}\) is at most \(11\cdot p = 11d/40 < d/3\). Since \(K\) is \(d/3\)-vertex-connected, \(K^-\) is connected.
Claim 2: for every \(v\in K^-\) and \(P\in \mathcal{P}\), \( \vert N_K(v)\cap V(P) \vert \leq 3\).
Suppose the claim is not true, then we can shortcut \(P\) via \(v\) to get a shorter path connecting the endpoints of \(P\), contradicting the minimality of \(\mathcal{P}\). See Figure 1(c).
Note that \(\delta(K)\geq d/3\) as it is \(d/3\)-connected. By Claim 2, \(\delta(K^-)\geq \delta(K) -3\cdot p \geq d/3 - 3d/30 \geq d/4\). The same argument in the detour above implies that \(K^-\) has diameter at most \(10\). Thus, there is a path of length at most \(10\) from \(s_1\) to \(t_1\) in \(K^-\), contradicting the maximality of \(\mathcal{P}\).
3. Optimal Sparsity: \(O(r\sqrt{\log{r}})\)
We assume that the graph has at least \(d\cdot n\) edges. Our goal is to construct a minor of size \(\Omega(d/\sqrt{\log d})\). By taking contrapositive, we obtain Theorem 1.
3.1. Proof Ideas
By Lemma 2, it suffices to construct a clique minor of size \(\Omega(d/\sqrt{\log d})\) for a \(d/3\)-vertex-connected graph \(K\) with at most \(2d\) vertices. In particular, we will construct a collection of \(h = d/(c_1 \sqrt{\log d})\) vertex-disjoint connected subgraphs \(C_1,C_2,\ldots, C_h\) such that (a) there is an edge between any two subgraphs \(C_i,C_j\) for \(1\leq i\not=j \leq h\) and (b) each \(C_i\) has \(O(c_0) \sqrt{\log d}\) vertices, for some constant \(1\ll c_0 \ll c_1\). These subgraphs will realize a \(K_h\)-minor of \(K\).
The choices of constants \(c_0\) and \(c_1\) imply that \( \vert V(C_1)\cup \ldots \cup V(C_h) \vert \leq d/12\). Thus, if we let \(H_i = K\setminus (C_1\cup \ldots \cup C_i)\) for any \(i\leq h\), then \(H_i\) is \(d/3 - d/12 = d/4\) vertex-connected. This in particular, implies that \(H_i\) has diameter at most \(22 = O(1)\).
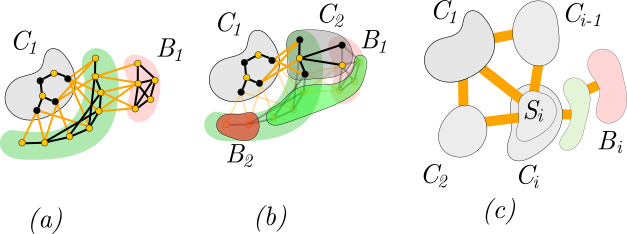
Figure 2: (a) \(C_1\) forms from \(S_1\), the set of black vertices, and its bad set \(B_1\). (b) \(C_2\) is constructed from \(S_2\) (black vertices), which avoids \(B-1\), and its bad set \(B_2\). (c) \(S_i\) has edges to all graphs \(C_1,C_2,\ldots,C_{i-1}\).
We will construct each \(C_i\) by random sampling. To gain intuition, let’s look at the first step: (1) sampling a set \(S_1\) of \(s = c_0\sqrt{\log n}\) vertices and (2) making \(S_1\) connected by adding a shortest path from one vertex to every other vertex in \(S_1\). See Figure 2 (a). There are two good reasons for doing this:
- As the graph has diameter \(O(1)\), \( \vert V(C_1) \vert = O(c_0 \sqrt{\log d})\).
- About \(e^{-O(c_0)\sqrt{\log d}}\cdot d\) vertices are not dominated by \(S_1\). This is because each vertex has at least \(d/3\) neighbors (as \(K\) is \(d/3\)-connected), and hence probability that a vertex is not dominated by \(S_1\) is at most \((1-d/(3\cdot 2d))^{s} = e^{-O(c_0)\sqrt{\log d}}\). Let’s call these vertices bad vertices (for a reason explained later), and denote the set of bad vertices by \(B_1\). (A vertex is donimated by \(S_1\) if it is in \(S_1\) or adajcent to another vertex in \(S_1\).)
The second step, we sample \(S_2\) in exactly the same way and make \(C_2\) by adding paths between vertices of \(S_2\). The graph we construct \(C_2\) now is \(H_1 = K\setminus V(C_1)\), and as argue above, \(H_1\) has roughly the same properties of \(K\): \(d/4\)-vertex-connected and diameter \(O(1)\). We want \(S_2\) to contain a vertex adjacent to \(S_1\) (in \(K\)) because we would like \(C_2\) to be adjacent to \(C_1\). That is, we want \(S_2 \not\subseteq B_1\): we say that \(S_2\) avoids bad set \(B_1\). See Figure 2(b). The reason 2 above implies that \(\mathrm{Pr}[S_2\subseteq B_1] \leq (e^{-O(c_0)\sqrt{\log d}})^{c_0\sqrt{\log d}} \leq 1/d^2\) for some chocie of \(c_0\gg 1\). Thus, w.h.p, \(S_2\) avoids \(B_1\).
In general, at any step \(i \in [1,h]\), we already constructed a set of \(i-1\) vertex-disjoint conected subgraphs \(C_1,C_2,\ldots C_{i-1}\), each is associated with a bad set (a set of non-neighbors). See Figure 2(c). We want to construct \(C_i\) by sampling a set \(S_i\) and adding paths between vertices of \(S_i\). By the same reasoning above for \(S_2\) and using the union bound, the probability that \(S_i\) is connected to all \(i-1\) subgraphs, i.e, \(S_i\) avoids all the \((i-1)\) bad sets, is at least \(1 - d/d^2 = 1-1/d > 0\). When \(i = h\), we obtain a \(K_h\) minor as desired.
Notation: for a given set \(S\subseteq V\) in a graph \(G = (V,E)\), denoted by \(B_G(S)\) be the set of vertices not dominated by \(S\). That is, \(B_G(S) = V\setminus (S\cup(\cup_{v\in S}N_G(v)))\).
We construct a set of subgraphs \(C_1,C_2,\ldots, C_h\) realizing a \(K_h\)-minor of \(K\), for \(h = d/(c_1 \sqrt{\log d})\), in \(h\) iterations as follows.
Initially, \(H_0 = K, B_0 = \emptyset\).
In \(i\)-th iteration, \(i\geq 1\), we find a set \(S_i\) of at most \(c_0\sqrt{\log d}\) vertices s.t (a) \( \vert B_{H_{i-1}}(S_i) \vert \leq 2de^{-c_0\sqrt{\log d}/8}\) and (b) \(S_i\) is connected to each of \(C_1,C_2,\ldots,C_{i-1}\) by an edge. Next, let \(C_i\) be obtained by adding shortest paths from an arbitrary vertex \(v\in S_i\) to every other vertex in \(S_i\setminus {v}\), and \(B_i= B_{H_{i-1}}(S_i)\). Then, we define \(H_i = H_{i-1}\setminus V(C_i)\) for the next iteration.
Finally, output \(C_1,C_2,\ldots, C_h\).
To show the correctness of the algorithm, we only have to show that the set \(S_i\) at iteration \(i\) exists, for some choices of \(1\ll c_0 \ll c_1\). If so, \(C_1,C_2,\ldots, C_h\) form a \(K_h\)-minor of \(K\), and hence, of \(G\).
First, we show that \(H_i\) has high connectivity and \(C_i\) has size \(O(c_0\sqrt{\log d})\).
Lemma 4: For every \(i\geq 1\), \( \vert V(C_i) \vert \leq 22 c_0\sqrt{\log d}\) and \(H_i\) is \(d/4\)-vertex connected when \(c_1 = 12c_0\).
Proof: We prove by induction. Since \(H_{i-1}\) is \(d/4\)-connected and \( \vert V(H_i) \vert \leq 2d\), the diameter of \(H_{i-1}\) is at most \(22\). As we add at most \(c_0\sqrt{\log d}\) shortest paths to \(S_i\), \( \vert V(C_i) \vert \leq 22 c_0\sqrt{\log d}\).
Observe that \(\sum_{j=1}^{i} \vert V(C_j) \vert \leq c_0\sqrt{\log d}\cdot h= c_0\sqrt{\log d} \cdot d/(c_1\sqrt{\log d}) = d/12\). Since \(K\) is \(d/3\)-vertex connected, \(H_i\) is \(d/3-d/12 = d/4\) vertex connected.
Now we show the existence of \(S_i\). Note that condition (b) is equivalent to that \(S_i\) avoids all the bad sets \(B_0,B_1,\ldots, B_{i-1}\). Let \(S_i\) be otabined by choosing each vertex of \(H_{i-1}\) with probability \(c_0\sqrt{\log d}/(2d)\); the expected size of \(S_i\) is a most \(c_0\sqrt{\log d}\). By Lemma 4, every vertex \(v\in H_{i-1}\) has degree at least \(d/4\). Thus, \(\mathrm{Pr}[v\in B_{i}]\leq (1-c_0\sqrt{\log d}/(2d))^{d/4}\sim e^{-c_0\sqrt{\log d}/8}\). In particular, \( \vert \mathbb{E}[B_i] \vert \leq (2d)e^{-c_0\sqrt{\log d}/8}\).
It remains to show that with non-zero probability, \(S_i\) avoids all \(B_0,\ldots, B_{i-1}\). Note that \( \vert V(H_{i-1}) \vert \geq d/4\). For a fixed \(j\in [0,i-1]\):
\(\mathrm{Pr}[S_i\subseteq B_j]\leq ( \vert B_j \vert / \vert V(H_{i-1}) \vert )^{ \vert S_j \vert }\leq 8(e^{-c_0\sqrt{\log d}/8})^{c_0\sqrt{\log d}}= 8e^{-c_0^2 \log(d)/8} \leq 1/d^2\)
for a sufficiently large \(c_0\geq 1\).
By union bound, the probability that \(\mathrm{Pr}[S_i\subseteq B_j]\) for some \(j\in [0,i-1]\) is at most \(h/d^2\leq 1/d\). Thus, the probability that \(S_i\) avoids all \(B_j\) is at least \(1-1/d\). This conclude the proof.
4. A Lower Bound
In this section, we show that for any \(n\) and \(r\) such that \(n \gg r\sqrt{\log r}\), there exists a graph \(G\) with \(n\) vertices and \(\Theta(n\cdot r\sqrt{\log r})\) edges such that \(G\) has no \(K_{r}\) minor. The key idea of the construction is Theorem 4 below.
Theorem 4: There exists a graph \(H\) with \(k\) vertices and \(\Theta(k^2)\) edges such that \(H\) has no \(K_s\)-minor where \(s = k/(\epsilon\sqrt{\log k})\) for some constant \(\epsilon\in (0,1)\).
Theorem 4 implies a sparsity lower bound \(\Omega(r\sqrt{\log r})\) as follows. Let \(G\) be the disjoint union of \(\Theta(n/(r\sqrt{\log r}))\) copies of the same graph in Theorem 4 with \(k = \Theta(r\sqrt{\log r})\) vertices. Then \( \vert E(G) \vert = \Theta(n/(r\sqrt{\log r}))k^2 = \Theta(n\cdot r\sqrt{\log r})\). As \(H\) excludes a clique minor of size \(k/(\epsilon\sqrt{\log k}) \leq r\) (by choosing the constant in the definition of \(k\) appropriately), \(G\) excludes \(K_r\) as a minor.
Theorem 4 can be proven by the probabilistic method. To gain some intuition of the proof, consider any fixed partition of \(V(H)\) into vertex-disjont subsets \({V_1,V_2,\ldots, V_{s}}\) of size \(\epsilon \sqrt{\log k}\) each. For this partition to realize a \(K_s\) minor, there must be an edge between every two vertex sets \(V_i,V_j\) for \(i\not=j\). The probability of this is:
\[(1-2^{-|V_i||V_j|})^ = (1-2^{-\epsilon ^2 \log(k)})^ \approx e^{-k^{2 - \epsilon^2}/\log(k)}\]
By the union bound over at most \(k^k\) such partitions, the probability of having a \(K_s\) minor is at most \(k^k e^{-k^{2 - \epsilon^2}/\log(k)} \rightarrow 0 \) when \(k \rightarrow +\infty\). In other words, the probability of not having a \(K_{s}\) minor is close to \(1\).
In the formal proof, one has to work with the fact that the subsets in the partition might not have the same size; this can be resolved by simple algebraic manipulation.
Proof of Theorem 4. Let \(H = G(k,1/2)\) where \(G(k,1/2)\) is the Erdős–Rényi random graph with probability \(p = 1/2\). We now show that the probability that \(H\) contains a \(K_s\) minor tends to \(0\) when \(k\rightarrow \infty\).
Recall that \(K_s\) is a minor of \(H\) if there is a set of non-empty, connected, and vertex-disjoint subgraphs \(\mathcal{C} = {C_1,C_2,\ldots, C_s}\) such that there is an edge in \(H\) connecting every two graphs \(C_i,C_j\) for \(1\leq i\not=j \leq s\).
We will bound the probability of exsiting such \(\mathcal{C}\). Observe that the number of (ordered) partitions of \( \vert V(H) \vert \) into \(s\) non-empty subset is at most:
\[\frac{k!}{s!}{k-1\choose s-1} <k^k\]
Fixed such a partition of \( \vert V(H) \vert \), denoted by \(\mathcal{P}\). Let \(n_i\) be the number of vertices in \(i\)-th set. The probability that there is an edge betwen two different sets \(i\) and \(j\) is \((1-2^{-n_i\cdot n_j})\). Thus, probability of having an edge between any two different sets of \(\mathcal{P}\) is:
\[\prod_{(i,j)}(1-2^{-n_i\cdot n_j}) \leq \prod_{(i,j)}e^{-2^{-n_i\cdot n_j}} = e^{-\sum_{(i,j)}2^{-n_i\cdot n_j}}\]
where the product and sum is over all unordered pairs \((i,j)\). This implies that:
\[\mathrm{Pr}[\mathcal{C} \text{ exists}] \leq k^k \cdot e^{-\sum_{(i,j)}2^{-n_i\cdot n_j}}\]
We now estimate \(\sum_{(i,j)}2^{-n_i\cdot n_j}\). By arithmetic–geometric mean inequality,
\(\sum_{(i,j)}2^{-n_i\cdot n_j}\geq {s \choose 2}\left(\prod_{(i,j)}2^{-n_i\cdot n_j}\right)^{1/{s\choose 2}} \geq {s \choose 2} \left(2^{-\sum_{(i,j)}n_i\cdot n_j}\right)^{1/{s\choose 2}}\)
Observe that \(\sum_{(i,j)}n_i\cdot n_j\) is the number of edges in a complete s-partite graph with \(k\) vertices. Thus, \(\sum_{(i,j)}n_i\cdot n_j\leq k^2/2\) and hence:
\[\sum_{(i,j)}2^{-n_i\cdot n_j} \geq {s \choose 2} 2^{-k^2/s^2}\]
Thus,
\[\mathrm{Pr}[\mathcal{C} \text{ exists}] \leq k^k \cdot e^{- {s \choose 2} 2^{-k^2/s^2}}\]
By chooosing \(s = ck/(\sqrt{\log k})\) for some big enough constant \(c\), we have \(\mathrm{Pr}[\mathcal{C} \text{ exists}] \rightarrow 0\) when \(k\rightarrow \infty\).
Bibliographical Notes
The exponential sparsity bound in Section is due to Reinhard Diestel (Proposition 7.2.1. [3]). The \(O(r^2)\) sparsity bound in Section 2 is obtained by a combination of various ideas, in particular, Lemma 1 is due to Exercise 21, Chapter 7, in [3], Lemma 2 is from the proof of Theorem 1 in [1], and Lemma 3 is a modification of Lemma 3.5.4 in [3].
Mader [5] proved a sparstiy bound \(O(r\log(r))\) for \(K_r\)-minor-free graphs. Kostacha was the first to show that the sparsity is \(\Theta(r\sqrt{\log r})\). Thomason [6] provided a more refined range for the sparsity bound: \([0.265r\sqrt{\log_2 r}(1+o(1)), 0.268r\sqrt{\log_2 r}(1+o(1))]\). The bound then was tightened exactly to \((\alpha +o(1))r\sqrt{\ln(r)}\) where \(\alpha = 0.319…\) is an explcit constant, also by Thomason [7]. The simpler proof presented in Section 3 is due to Alon, Krivelevich, and Sudakov [1].
The lower bound in Section 4 is due to Bollobás, Catlin, and Erdös [2].
References
[1] Alon, N., Krivelevich, M., and Sudakov, B. (2022). Complete minors and average degree–a short proof. ArXiv preprint arXiv:2202.08530.
[2] Bollobás, B., Catlin, P. A., and Erdös, P. (1980). Hadwiger’s conjecture is true for almost every graph. Eur. J. Comb., 1(3), 195-199.
[3] Diestel, R. (2017). Graph theory. Springer.
[4] Kostochka, A. V. (1982). A lower bound for the Hadwiger number of a graph as a function of the average degree of its vertices. Discret. Analyz. Novosibirsk, 38, 37-58.
[5] Mader, W. (1968). Homomorphiesätze für graphen. Mathematische Annalen, 178(2), 154-168.
[6] Thomason, A. (1984). An extremal function for contractions of graphs. In Mathematical Proceedings of the Cambridge Philosophical Society (Vol. 95, No. 2, pp. 261-265). Cambridge University Press.
[7] Thomason, A. (2001). The extremal function for complete minors. Journal of Combinatorial Theory, Series B, 81(2), 318-338.
]]> Figure 1: A Steiner-free tree cover with 2 trees for \(T\) on the left. The distortion is \(\alpha = 4/3\) realized by the vertex pair \({e,g}\).
Figure 1: A Steiner-free tree cover with 2 trees for \(T\) on the left. The distortion is \(\alpha = 4/3\) realized by the vertex pair \({e,g}\).